Transformer 구현 Issue 정리

Introduction

PyTorch로 Transformer을 구현하며 생기는 issue를 정리해보았다. 구현한 repo는 다음을 참고.

우선 구조 이야기를 해보겠다. 고민이 제일 많이 되었던 부분인데, Transformer를 먼저 만들고, 그 안에서 encoder와 decoder, 또 다시 encoder 안에서 multiheadattn 등을 만드는 식으로 잡았다. 너무 클래스간 결합성이 낮나 싶을 정도로 잘라놓긴 했다. 그래서 별 필요없는 parameter도 여러번 걸쳐서 scaled dop product attention까지 들어간다. 그래도 뭐 좋은게 좋은거니까…

sequence length는 미리 정해야 하는가?

Seq2Seq은 RNN에서 알아서 반환해주니까 sequence length를 따로 생각할 필요가 없었다. 그러나 트랜스포머는 그런 구조가 아니므로 sentence의 길이를 미리 정해놓고 가야 하는지 의문이 생겼다. 아주 당연하게도, 정답은 당연히 그래야 한다. 따라서 추후에 padding도 해야한다.

positional encoding을 어떻게 구현하는가?

우선, 내가 착각하고 있는게 있었는데, 난 여태까지 $PE_{(pos, 2i)} = sin({(\frac{pos}{10000}})^{\frac {2i} {d_{model}}})$ 인 줄 알았다. 근데 알고보니 $PE_{(pos, 2i)} = sin({\frac{pos}{10000^{\frac {2i} {d_{model}}}}})$ 였었다.

논문만 읽었을 땐 그냥 지나쳤는데, 막상 구현하려니 난감했다. pos랑 i 모두 신경써야 했기 때문이다. 도저히 혼자 힘으로 짜기가 어려워서 하버드에서 나온 자료를 보고 한 번 따라해봤다.

우선 pe를 [S, D_model]로 초기화한다. Batch 단위로 합쳐주면 되기 때문에, 굳이 여기서 신경 쓸 필요는 없다.

>>> pe = torch.zeros(max_len, d_model)
>>> pe
tensor([[0., 0., 0., 0., 0., 0., 0., 0.],
        [0., 0., 0., 0., 0., 0., 0., 0.],
        [0., 0., 0., 0., 0., 0., 0., 0.],
        [0., 0., 0., 0., 0., 0., 0., 0.],
        [0., 0., 0., 0., 0., 0., 0., 0.],
        [0., 0., 0., 0., 0., 0., 0., 0.],
        [0., 0., 0., 0., 0., 0., 0., 0.],
        [0., 0., 0., 0., 0., 0., 0., 0.],
        [0., 0., 0., 0., 0., 0., 0., 0.],
        [0., 0., 0., 0., 0., 0., 0., 0.]])

이 후, [S, 1]짜리 tensor($pos$)를 만들어서, pe와 더해준다. 그러면 broadcasting이 되면서 element-wise로 더해진다.

>>> pos = pos = torch.arange(0, max_len).unsqueeze(1).float()
>>> pe + pos
tensor([[0., 0., 0., 0., 0., 0., 0., 0.],
        [1., 1., 1., 1., 1., 1., 1., 1.],
        [2., 2., 2., 2., 2., 2., 2., 2.],
        [3., 3., 3., 3., 3., 3., 3., 3.],
        [4., 4., 4., 4., 4., 4., 4., 4.],
        [5., 5., 5., 5., 5., 5., 5., 5.],
        [6., 6., 6., 6., 6., 6., 6., 6.],
        [7., 7., 7., 7., 7., 7., 7., 7.],
        [8., 8., 8., 8., 8., 8., 8., 8.],
        [9., 9., 9., 9., 9., 9., 9., 9.]])

그 다음은 idx를 만들 차례이다. 위 수식에서의 i를 의미한다. 이는 짝수/홀수에 대해 broadcasting 할 것이므로, d_model의 절반만큼만 만들어준다.

>>> idx = torch.arange(0, d_model, 2).float()
>>> idx /= d_model
>>> idx = 1/10000 ** idx
>>> idx
tensor([1.0000, 0.1000, 0.0100, 0.0010])

그 다음은 pe에 idx를 곱해주는 일만 남았다. 여기서 $2i$/$2i+1$만큼을 slicing 한다.

pe[:, 0::2] = torch.sin(pe[:, 0::2] * idx)
pe[:, 1::2] = torch.cos(pe[:, 0::2] * idx)
>>> pe
tensor([[ 0.0000,  1.0000,  0.0000,  1.0000,  0.0000,  1.0000,  0.0000,  1.0000],
        [ 0.8415,  0.6664,  0.1769,  0.9995,  0.0316,  1.0000,  0.0056,  1.0000],
        [ 0.9093,  0.6143,  0.3482,  0.9981,  0.0632,  1.0000,  0.0112,  1.0000],
        [ 0.1411,  0.9901,  0.5085,  0.9959,  0.0947,  1.0000,  0.0169,  1.0000],
        [-0.7568,  0.7270,  0.6528,  0.9933,  0.1262,  1.0000,  0.0225,  1.0000],
        [-0.9589,  0.5744,  0.7765,  0.9905,  0.1575,  1.0000,  0.0281,  1.0000],
        [-0.2794,  0.9612,  0.8757,  0.9879,  0.1886,  1.0000,  0.0337,  1.0000],
        [ 0.6570,  0.7918,  0.9473,  0.9858,  0.2196,  1.0000,  0.0394,  1.0000],
        [ 0.9894,  0.5492,  0.9890,  0.9846,  0.2503,  1.0000,  0.0450,  1.0000],
        [ 0.4121,  0.9163,  0.9996,  0.9842,  0.2808,  1.0000,  0.0506,  1.0000]])

위 링크의 자료에서는 이거보다 짧게 구현했지만 난 머리가 좋지 않아서 풀어쓰는게 좋다. 여튼 이해됐으면 됐지 뭐.

module을 복사할 때 deepcopy를 쓸까? 아니면 객체를 생성할까?

Encoder 같은 경우에는 a stack of $N = 6$ identical layers 라고 본문에 명시되어 있다. 따라서 iteration을 통해서 encoder를 매번 생성해서 Encoders라는 nn.Sequential에 add_module()을 통해 넣는 것으로 설정했다. 다른 사람들의 implementation을 보면, deepcopy를 사용하는 경우가 많았는데, 굳이 그래야 하는 의문이 든다.

근데 PyTorch에서 nn.Sequential을 쓰면 parameter를 여러개를 쓸 수가 없다. 그래서 Modulelist 내에서 comprehension으로 만들어줬다.

만일 따로 만들어준다면, OOP, 혹은, 기능에 따라 함수를 구현하는 것으로 이해할 수 있을 것 같다.

Scaled Dot Product Attention class가 따로 필요한가?

본문에는 input으로 q, k, v를 받는다고 되어 있다. 따라서 forward에서 얘네 셋을 받아줬다. 그러면 의문이 생기는게… 여기서 하는 일은 그냥 attention score 계산하는 거 밖엔 없다. 따라서 기능상으로는 필요한 구조가 아니다 (그러나 객체지향적으론 옳아보인다). 거기다가 q, k, v는 각 attention으로 동시에 들어가기 때문에 이걸 따로 구현하는게 애매하다고 생각했다. 따라서 그냥 MultiHeadAttn을 만들고, 한꺼번에 넣어주는 것으로 생각했다. 그리고 각 attention layer는 필요하다면 따로 get 메소드를 통해서 받으면 될 것 같다.

사실 여기서 더 생각해보면, Q, K, V에 대한 weight를 전부 다 합친, $W \in R^{Batch \times \textrm{Seq_len} \times \textrm{3d_model}}$을 생각할 수 있을 것 같다. 이 경우 linear 모델에 bias가 없는 경우를 생각할 수 있을 것 같다.

W_q, W_v, W_k의 size는 어떻게 정해야 하는가?

embedding vector의 사이즈는 [Batch x Seq_len x d_model]이고, 각 어텐션을 통과하면 [Batch x Seq_len x d_model/h]가 된다. 나는 Scaled Dot Product Attention을 따로 구현하지 않았기 때문에 [Batch x Seq_len x d_model]이 될 것이다. 따라서, square matrix로 구현하면 된다.

이것도 잘 보면 논문에 다 나와있다. $W^Q_i \in R^{d_{model}\times d_k}$, $W^K_i \in R^{d_{model}\times d_k}$, $W^V_i \in R^{d_{model}\times d_v}$, $W^O \in R^{h d_v \times d_{model}}$ 이다.

그리고 굳이 nn.Parameter()로 구현할 필요가 없이, nn.Linear로 구현하면 된다. 실제로 하버드 구현은 nn.Linear로 되어 있다. 저번에 attention 구현했을 때와 마찬가지로 bias는 포함하면 될 것 같다.

Add & Norm은 뭐지?

Add & Norm은 $\textrm{LayerNorm}(x + \textrm{Sublayer}(x))$ 으로 계산된다. LayerNorm은 논문을 보면 되고, 안에는 residual connection이 되어있다. PyTorch에는 nn.LayerNorm으로 구현되어 있다. 듣자하니 RNN에서는 BN보다 더 낫다고 한다.

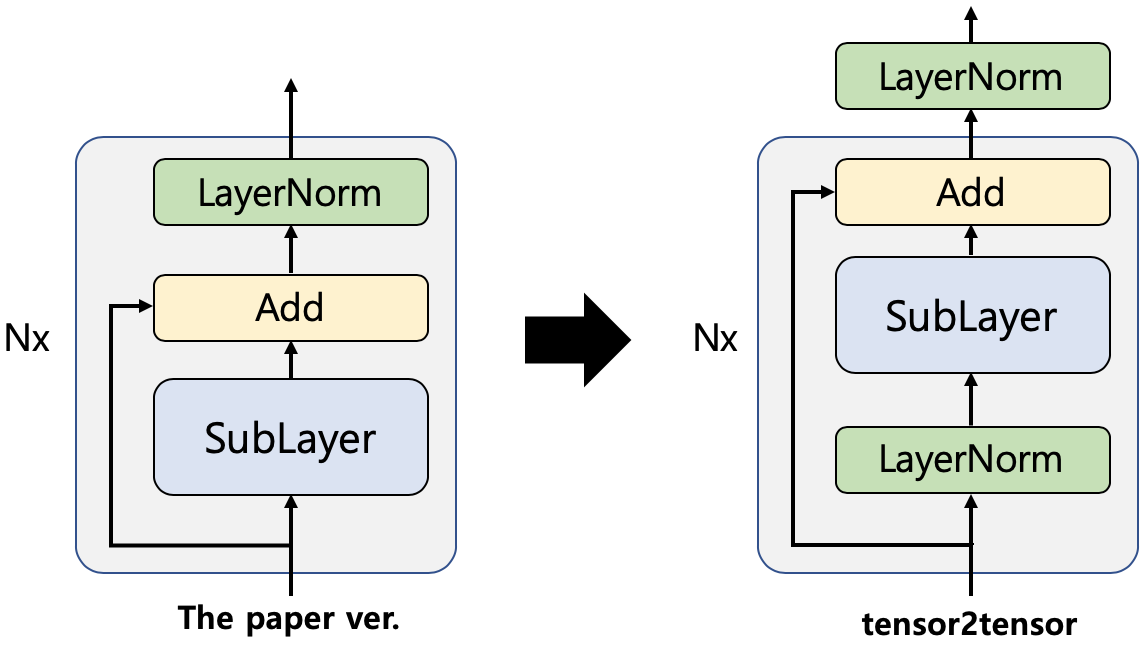
다만, 원래 paper와는 다르게 실제로 구현할 때는 layer norm의 순서가 약간 다르다. 대부분의 구현은 아래의 그림처럼 되어있는데, 성능이 더 좋기 때문이다. 자세한 내용은 다음을 참고.

Position-wise FFN에서 inner-layer dimensionality가 무엇인가?

본문에 보면, the inner-layer has dimensionality $d_{ff}=2048$이라고 되어 있다. FC가 2개 이므로, 처음에 있는 FC의 weight가 [512 x 2048]이고, ReLU를 거친 FC가 [2048 x 512] 인 것으로 보인다.

dropout은 어디에 사용되는가?

다음을 참고한 결과, 논문에 나왔던데로 sub-layer, embedding layer 다음에 drop-out을 추가하고, 논문에 나오지는 않았지만, 일반적으로 사용하는 Position-wise FC의 ReLU 이후와 attention의 softmax 이후에도 추가적으로 사용하면 된다.

The paper described only two dropouts: one in the output of each sub-layer and the other in the embedding layers. But, two more dropouts are added to Transformer. Transformer has dropouts after ReLU in position-wise feed-forward networks, and after SoftMax in attentions.

positional encoding의 저장문제

앞서 positional_encoding을 다룬 하버드 자료에서는 self.register_buffer에 pe를 할당하는 모습을 볼 수 있다. register_buffer는 nn.Paramter와는 다르게, gradient가 흐르지는 않지만, nn.Module의 state_dict에 저장할 필요가 있을 때 쓰인다. 예를 들면 batch norm같은게 있다. 그러면 여기서 드는 의문은 pe는 언제 저장해야 하는가?

앞서 Transforemr에서 정의한다고 되어있는데, 이렇게 되면 initializer에서 초기화 및 계산을 시행해줘야 하므로 따로 클래스로 만들었다. gradient는 흐르지 않지만, PositionalEncoding 내에서도 buffer에 등록해야 하므로, nn.Module을 상속하였다. 그리고 임베딩 레이어 이후에 저장하는 것으로 해결했다.

재미있는 점은 self.register_buffer로 등록하면, 자동으로 instance의 attribute로 등록된다는 점이다.

src_mask가 왜 필요하지?

PyTorch 문서를 보면 forward에 src_mask에 해당하는 parameter가 있다. 이게 왜 필요하지 싶어서 알아보았는데, <pad> token을 위해서였다. 패드 토큰은 attention weight에 영향을 주면 안되므로, 이를 0으로 처리한다.

-1e9 vs. -2e9

보통 무한대를 나타낼 때 2e9를 통해 나타내는 것으로 알고 있다. 그러나 대부분의 implementation은 1e9를 사용하는데, 이는 overflow를 막기 위함이다.

Dropout layer를 재사용해도 되는가?

안됨. 다음을 참고.

Labeling Smoothing module 만들기

두 가지 문제가 있는데, 첫 번째로 Labeling Smoothing이 뭔지 모르겠고, 두 번째는 pytorch에서 custom loss를 짜는 방법을 모르겠다.

Labeling Smoothing란?

Label smoothing은 regularization 기법 중 하나로, 말 그대로 label을 smoothing하는 기법이다. one-hot representation으로 이루어진 hard target을 soft target으로 바꾸는 것으로, model calibration 효과가 있다.

$K$개 class에 대한 labeling smoothing vector의 $k$번째 sclar값은 다음과 같다.

\[y^{LS}_k = y_k(1-\alpha) + alpha/K\]

여기서 $y_k$는 $k$번째 class가 정답이면 1, 아니면 0이며, $\alpha$는 hyper parameter이다.

Custom loss in PyTorch

특별한 구현 없이 nn.Module내에서 계산하면 알아서 loss를 계산한다.

Beam Search

우선, Beam search가 inference외에 train/test에도 사용되는지 의문이었다. 그래서 한번 찾아봤더니, Beam Search Optimization(BSO)라는 개념이 있었다. 이는 RNN의 beam search 과정에서 training을 원할하게 하기 위해 loss function을 조정하는 개념이다. Transformer에선 inference시에만 하는 것으로 추정된다. (명확하게 밝혀지지 않아서 확실히 모르겠다)

아래는 이에 대한 정리이다.

• 그 유명한 word piece 논문을 참고
• decoding과정에서 socre function $s(Y,X)$를 maximize하는 sequence $Y$를 찾는 것이 목적
• Hyper parameter: dev set으로 얻음
• beam size: 4
  • 이게 없으면 모델은 더 짧은 문장을 선호
    • negative log-probability를 사용하는데, 길이가 길수록, 더 negative (lower)한 값이 나오기 때문
  • 공식은 다음과 같음
    • $s(Y,X)=log(P(Y \rvert X))/lp(Y)+cp(X;Y)$
    • $lp(Y)=\frac{(5+ \rvert Y \rvert)^\alpha}{(5+1)^\alpha}$
      • $ \rvert Y \rvert$는 Y의 length
      • $5$는 minimum length로, 이 또한 조정 가능
    • $cp(X;Y)=\beta*\sum^{\lvert X \rvert} _{i=1} log(min(\sum^{\lvert Y \rvert} _{j=1} p _{i,j} ,1.0))$
      • $p_{i,j} $는 i번째 source word $x_i$에 대한 j번째 target word $y_j$ attention probability
    • Attention 확률의 합은 1이 되므로, $\sum^{\rvert X \rvert}p_{i,j}=1$
    • $\alpha, \beta$는 length normalization과 coverage penaly를 관리하는 parameter
      • $\alpha=0,\beta=0$이면, 일반적인 beam search
  • 논문에선 length penalty $\alpha=0.6$로 설정
  • coverage penalty는 사용하지 않은 것으로 보임

추가자료: Convnet as Feedforward

원문에는 feedforward 대신 convolution filter를 2개 중첩할 수도 있다는 이야기가 있다.

While the linear transformations are the same across different positions, they use different parameters from layer to layer. Another way of describing this is as two convolutions with kernel size 1.

그러나 이 글을 보면 꼭 그렇지도 않은것으로 보인다. 다만 특별한 task에 따라 kernel size를 다르게 하면 성능이 올라가는 것으로 보인다. 다음에선 다음과 같이 설명하고 있다.

In fact for the sequence tagging task we use convolutions instead of fully connected layers. A filter of width 3 allows interactions to happen with adjacent time steps to improve performance. The implementation in PyTorch is straightforward: